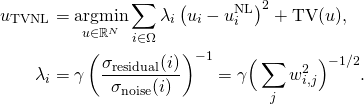In order to provide a fully automatic denoising algorithm, we have developed an automatic noise estimation method that relies on the non-parametric detection of homogeneous areas. First, the homogeneous regions of the image are detected by computing Kendall’s rank correlation coefficient [1]. Computed on neighboring pixel sequences, it indicates the dependancy between neighbors, hence reflects the presence of structure inside an image block. This test is non-parametric, so the performance of the detection is independant of the noise statistical distribution. Once the homogeneous areas are detected, the noise level function, i.e., the function of the noise variance with respect to the image intensities, is estimated as a second order polynomial minimizing the ![]() error on the statistics of these regions.
error on the statistics of these regions.
Matlab implementation of the noise estimation algorithm
Related papers:
– C. Sutour, C.-A. Deledalle et J.-F. Aujol. Estimation of the noise level function based on a non-parametric detection of homogeneous image regions. Submitted to Siam Journal on Imaging Sciences, 2015.
– C. Sutour, C.-A. Deledalle et J.-F. Aujol. Estimation du niveau de bruit par la détection non paramétrique de zones homogènes. Submitted to Gretsi, 2015.
References
[1] Buades, A., Coll, B., and Morel, J.-M. (2005). A review of image denoising algorithms, with a new one. Multiscale Modeling and Simulation, 4(2): 490–530.