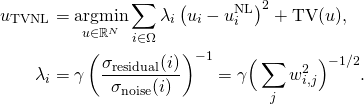The denoising algorithm that has been developed is based on an adaptive regularization of the NL-means [1]. The proposed model is the following:
(1) 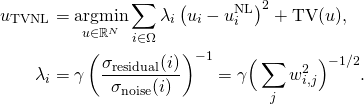
where 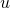 is the solution obtained with the NL-means algorithm, TV refers to the total variation of the image and
is the solution obtained with the NL-means algorithm, TV refers to the total variation of the image and 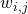 is the weight that measures the similarity between the patch of index
is the weight that measures the similarity between the patch of index 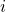 and the patch of index
and the patch of index 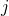 in the NL-means algorithm. The ratio
in the NL-means algorithm. The ratio 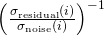 reflects the noise variance reduction performed by the NL-means. This formulation allows locally adaptive regularization of the NL-means solution
reflects the noise variance reduction performed by the NL-means. This formulation allows locally adaptive regularization of the NL-means solution 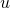 , thanks to a confidence index
, thanks to a confidence index 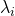 that reflects the quality of the denoising performed by the NL-means.
that reflects the quality of the denoising performed by the NL-means.
This model can be adapted to the different noise statistics belonging to the exponential family (Gaussian, Poisson, multiplicative…). It can also be adapted to video denoising thanks to the use of 3D patches combined to a spatio-temporal TV regularization.
Matlab implementation of RNL
Results of video denoising with R-NL and comparisons
Related papers:
1. C. Sutour, C.-A. Deledalle et J.-F. Aujol. Adaptive regularization of the NL-means : Application to image and video denoising. IEEE Transactions on image processing, vol. 23(8) : 3506-3521, 2014.
2. C. Sutour, J.-F. Aujol, C.-A. Deledalle et J.-P. Domenger. Adaptive regularization of the NL-means for video denoising. International Conference on Image Processing (ICIP), pages 2704–2708. IEEE, 2014.
3. C. Sutour, J.-F. Aujol et C.-A. Deledalle. TV-NL : Une coopération entre les NL-means et les méthodes variationnelles. Gretsi, 2013.
References
[1] Buades, A., Coll, B., and Morel, J.-M. (2005). A review of image denoising algorithms, with a new one. Multiscale Modeling and Simulation, 4(2): 490–530.